Xin chào các bạn! Trong bài đầu tiên của toán học 12 chúng ta sẽ học về tính đơn điệu của hàm số. Thông tin chi tiết bài sự đồng biến, nghịch biến của hàm số sẽ được Hocvahoi.com chi tiết trong bài viết dưới đây. Mời các bạn, các thầy cô cùng xem để có kiến thức tổng quát nhất.
A: Lý thuyết sự đồng biến nghịch biến của hàm số
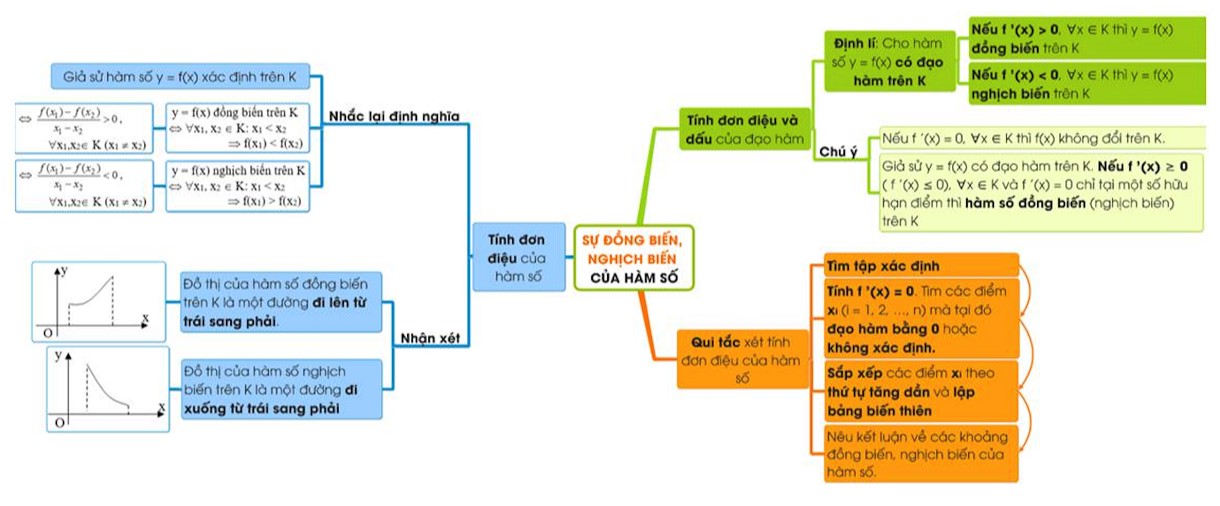
→ K là ký hiệu của một khoảng, một đoạn hay một nửa khoảng.
1. Định nghĩa
Hàm số y = f(x) đồng biến (tăng) trên K ⇔ với ∀x1, x2 ∈ K, x1 < x2 thì f(x1) < f(x2).
Hàm số y = f(x) nghịch biến (giảm) trên K ⇔ với ∀x1, x2 ∈ K, x1 < x2 thì f(x1) > f(x2).
2. Điều kiện cần để cho hàm số đơn điệu
Cho hàm số f có đạo hàm trên K.
– Nếu hàm số f đồng biến trên K thì f'(x) ≥ 0 với mọi x ∈ K.
– Nếu hàm số f nghịch biến trên K thì f'(x) ≤ 0 với mọi x ∈ K.
3. Điều kiện đủ để cho hàm số đơn điệu
Cho hàm số f có đạo hàm trên K.
- Nếu f'(x) > 0 với mọi x ∈ K thì hàm số f đồng biến trên K.
- Nếu f'(x) < 0 với mọi x ∈ K thì hàm số f nghịch biến trên K.
- Nếu f'(x) = 0 với mọi x ∈ K thì hàm số f là hàm hằng trên K.
Định lý mở rộng
- Nếu f'(x) ≥ 0 với mọi x ∈ K và f'(x) = 0 chỉ tại một số hữu hạn điểm thuộc K thì f sẽ đồng biến trên K.
- Nếu f'(x) ≤ 0 với mọi x ∈ K và f'(x) = 0 chỉ tại một số hữu hạn điểm thuộc K thì f sẽ nghịch biến trên K.
4. Những quy tắc xét tính đơn điệu của hàm số
i) Tìm tập xác định
ii) Tính đạo hàm f'(x). Tìm các điểm xi (i= 1, 2 ,…, n) mà tại đó đạo hàm của chúng bằng 0 hoặc không xác định
iii) Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên.
iv) Nêu kết luận về các khoảng đồng biến và nghịch biến của hàm số.
B: Tính đơn điệu của hàm số
1. Định nghĩa về tính đơn điệu của hàm số:
Hàm số f xác định trên K. Với mọi x1,x2 thuộc K mà x1>x2
- Nếu f(x1)>f(x2) thì hàm số f tăng trên K
- Nếu f(x1)<f(x2) thì hàm số f giảm trên K.
Chú ý:
- Hàm số tăng hoặc giảm trên K thì được gọi chung là hàm số đơn điệu trên K.
- Ký hiệu K có thể là một khoảng, một đoạn hoặc một nửa khoảng.
2. Điều kiện cần để hàm số đơn điệu
Cho một hàm số f có đạo hàm trên khoảng K
- Nếu f tăng trên K thì f′(x)>0, với mọi x thuộc khoảng K.
- Nếu f giảm trên K thì f′(x)<0, với mọi x thuộc khoảng K.
3. Điều kiện đủ để hàm số đơn điệu
Cho một hàm số f có đạo hàm trên một khoảng K
- Nếu f′(x)>0 với mọi x thuộc K thì f tăng trên khoảng K.
- Nếu f′(x)<0 với mọi x thuộc K thì f giảm trên khoảng K.
Chú ý: Nếu f′(x)≥0 với ∀x∈K hoặc f′(x)≤0 với ∀x∈K và f′(x)=0 chỉ tại một số hữu hạn điểm thuộc khoảng K thì hàm số f tăng (hoặc giảm) trên K.
C: Trả lời câu hỏi và giải bài tập SGK Toán 12 bài 1
Trả lời câu hỏi 1 trang 4 SGK Giải tích 12 tập 1:
Đề bài:

- Trên khoảng K: đồ thị của hàm số đi lên (từ trái sang phải) thì hàm số đồng biến trên K.
- Trên khoảng K: đồ thị của hàm số đi xuống (từ trái sang phải) thì hàm số nghịch biến trên K.
Lời giải chi tiết:
– Hàm số: y = cos x trên đoạn \frac{3π}{2}$$ ; \frac{3π}{2}$$]
Các khoảng tăng:
Các khoảng giảm: (0; π)
Hàm số y=|x| trên khoảng (−∞;+∞)
Các khoảng tăng: (0,+∞): do đồ thị hàm số đi lên trong khoảng đó cho nên nếu x tăng thì y cũng tăng.
Khoảng giảm (−∞, 0): do đồ thị hàm số đi xuống trong khoảng đó nên khi x tăng thì y giảm.
